
| Cool stuff! Try out the ten interactive self-test exercises at the bottom of this page! |
Just as organic chemists have their octet rule for organic compounds, so do organometallic chemists have the 18 electron rule. And just as the octet rule is often violated, so is the 18 electron rule. However, both serve a useful purpose in predicting reactivity. Each derives from a simple count of the number of electrons that may be accommodated by the available valence orbitals (one s and three p for organic chemists; organometallic chemists get five bonus d-orbitals in which to place their electrons).
Knowing how many valence electrons "belong to" a transition metal complex allows us to make predictions about the mechanisms of reactions and the possible modes of reactivity. There are two distinct methods that are used to count electrons, the neutral or covalent method and the effective atomic number or ionic method. While this may seem confusing, these are simply two different accounting systems that give us the same final answer. Although having two systems may seem confusing, it at least provides us a convenient way to double check our answer.
While we teach our students in freshman chemistry that the periodic table is filled in the order [Ar]4s23d10, this turns out to be true only for isolated metal atoms. When we put a metal ion into an electronic field (surround it with ligands), the d-orbitals drop in energy and fill first. Therefore, the organometallic chemist considers the transition metal valence electrons to all be d-electrons. There are certain cases where the 4s23dx order does occur, but we can neglect these in our first approximation.
Therefore, when we ask for the d-electron count on a transition metal such as Ti in the zero oxidation state, we call it d4, not d2. For zero-valent metals, we see that the electron count simply corresponds to the column it occupies in the periodic table. Hence, Fe is in the eighth column and is d8 (not d6) and Re3+ is d4 (seventh column for Re, and then add 3 positive charges...or subtract three negative ones). Now that we can assign a d-electron count to a metal center, we are ready to determine the electronic contribution of the surrounding ligands and come up with our overall electron count.

The basic premise of this method is that we remove all of the ligands from the metal and, if necessary, add the proper number of electrons to each ligand to bring it to a closed valence shell state. For example, if we remove ammonia from our metal complex, NH3 has a completed octet and acts as a neutral molecule. When it bonds to the metal center it does so through its lone pair (in a classic Lewis acid-base sense) and there is no need to change the oxidation state of the metal to balance charge. We call ammonia a neutral two-electron donor.
In contrast, if we remove a methyl group from the metal and complete its octet, then we formally have CH3-. If we bond this methyl anion to the metal, the lone pair forms our metal-carbon bond and the methyl group acts as a two-electron donor ligand. Notice that to keep charge neutrality we must oxidize the metal by one electron (i.e. assign a positive charge to the metal). This, in turn, reduces the d-electron count of the metal center by one. We'll see several examples below.
The major premise of this method is that we remove all of the ligands from the metal, but rather than take them to a closed shell state, we do whatever is necessary to make them neutral. Let's consider ammonia once again. When we remove it from the metal, it is a neutral molecule with one lone pair of electrons. Therefore, as with the ionic model, ammonia is a neutral two electron donor.
But we diverge from the ionic model when we consider a ligand such as methyl. When we remove it from the metal and make the methyl fragment neutral, we have a neutral methyl radical. Both the metal and the methyl radical must donate one electron each to form our metal-ligand bond. Therefore, the methyl group is a one electron donor, not a two electron donor as it is under the ionic formalism. Where did the other electron "go"? It remains on the metal and is counted there. In the covalent method, metals retain their full complement of d electrons because we never change the oxidation state from zero; i.e. Fe will always count for 8 electrons regardless of the oxidation state and Ti will always count for four.
Notice that this method does not give us any immediate information about the formal oxidation state of the metal, so we must go back and assign that in a separate step. For this reason, many chemists (particularly those that work with high oxidation state complexes) prefer the ionic method.

In the table below are some common transition metal ligands and the number of electrons that each donates to a metal center. Some ligands can donate a variable number of electrons. For example, an alkoxide, M-OR, can donate two to six electrons depending on the hybridization of the oxygen atom.
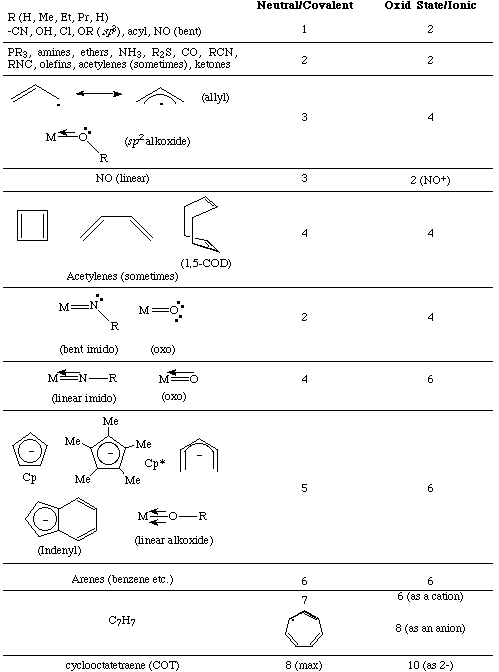

The most critical point we should remember is that like oxidation state assignments, electron counting is a formalism and does not necessarily reflect the distribution of electrons in the molecule. However, these formalisms are very useful to us, and both will give us the same final answer.
Consider the following simple examples. Notice how some ligands donate the same number of electrons no matter which formalism we choose, while the number of d-electrons and donation of the other ligands can differ. All we have to do is remember to be consistent and it will work out for us.
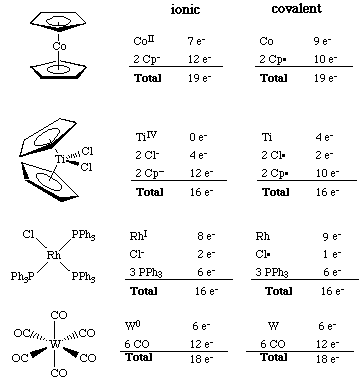

In each of the following examples, select the oxidation state of the transition metal atom, dn count (assign it using the ionic model), and number of valence electrons at each metal center. Then hit the Submit Answer button for that compound to see if you are correct.
If you do not yet know your periodic table, you can either visit the Periodic Table Challenge to test your skill or you can view a complete periodic table in this popup window.
THESE QUIZZES ARE NOT CURRENTLY WORKING - We moved to a new server platform in September 2025 and I have to go back and redo the coding that drives the grading. Stay tuned...