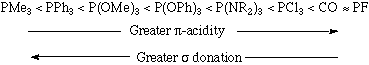Phosphine ligands have the general formula PR3 where R = alkyl, aryl, H, halide etc. Closely related are phosphite ligands which have the general formula P(OR)3.
Both phosphines and phosphites are neutral two electron donors that bind to transition metals through their lone pairs. There are many examples of polydentate phosphine ligands, some common examples of which are shown below. Furthermore, a variety of chiral phosphine transition metal complexes have been synthesized; these phosphine-metal complexes are stereogenic and can function as stereospecific catalysts. Some typical phosphine ligands are shown below:
While phosphine ligands are ubiquitous in transition metal chemistry and afford extremely reactive and versatile homogeneous catalysts, a process called phosphine degradation tends to limit their industrial application. Phosphine degradation typically involves an oxidative addition of the phosphine ligand which deactivates the metal center towards further catalysis.

Phosphines are easy to synthesize and are excellent ligands for transition metals. As a consequence, the steric attributes of the phosphine ligand are easily controlled. This ability to control the bulk of the ligand permits one to tune the reactivity of the metal complex. For example, if the dissociation of a phosphine ligand is the first step in a reaction, the reaction can be accelerated by utilizing a larger phosphine ligand. Likewise, if dissociation is a problem, then a smaller phosphine can be used.
Cone angles for some common phosphine ligands are:
| Phosphine Ligand | Cone Angle |
|---|---|
| PH3 | 87o |
| PF3 | 104o |
| P(OMe)3 | 107o |
| PMe3 | 118o |
| PMe2Ph | 122o |
| PEt3 | 132o |
| PPh3 | 145o |
| PCy3 | 170o |
| P(t-Bu)3 | 182o |
| P(mesityl)3 | 212o |
Take a look at these ball and stick models of various phosphine ligands to get a better idea of their steric attributes. Notice how the phosphites have smaller cone angles than their corresponding phosphines because the oxygen atoms act as "spacers".

The bonding in phosphine ligands, like that of carbonyls can be thought of as having two important components. The primary component is sigma donation of the phosphine lone pair to an empty orbital on the metal. The second component is backdonation from a filled metal orbital to an empty orbital on the phosphine ligand. This empty phosphorous orbital has been described as being either a d-orbital or an antibonding sigma orbital; current consensus is that the latter is more appropriate given the relatively high energy of a phosphorous d-orbital:
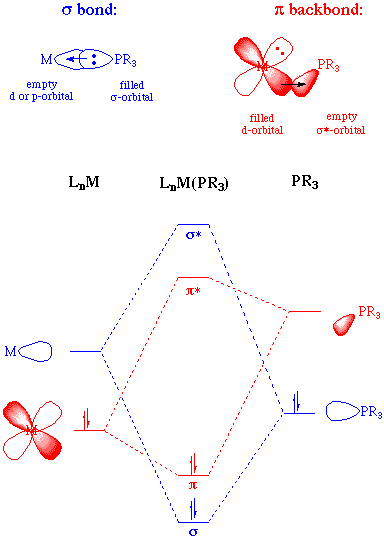
As electron-withdrawing (electronegative) groups are placed on the phosphorous atom, the sigma-donating capacity of the phosphine ligand tends to decrease. At the same time, the energy of the pi-acceptor (sigma-*) on phosphorous is lowered in energy, providing an increase in backbonding ability. Therefore, phosphines can exhibit a range of sigma donor and pi-acceptor capabilities, and the electronic properties of a metal center can be tuned by the substitution of electronically different but isosteric phosphines.
A rough ordering of the pi-accepting or sigma-donating capabilities of phosphines can be accomplished by synthesizing a series of complexes in which the only difference is the nature of the phosphine ligand. If these complexes contain a carbonyl ligand, then the CO stretching frequency can be used as an indicator of electron density at the metal (the lower the value of the CO stretching frequency, the greater the backbonding to the metal and thus the higher the electron density at the metal). Experiments such as this permit us to come up with the following empirical ordering: